“π” ദിനം.
അങ്ങനെയും ഒരു ദിനമോ! ചിലരെങ്കിലും നെറ്റി ചുളിക്കുന്നുണ്ടാവും. അതെ അങ്ങനെയും ഒന്നല്ല, രണ്ടു ദിനങ്ങള്. മാര്ച്ച് പതിനാലും ജൂലൈ ഇരുപത്തിരണ്ടും.
എല്ലാവരുടേയും നാവിന്തുമ്പിലുണ്ടാവും വൃത്തത്തിന്റെ പരിധി കണ്ടുപിടിക്കാനുള്ള
സൂത്രവാക്യം .
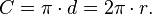
ഇതില് r വൃത്തത്തിന്റെ ആരത്തേയും d വ്യാസത്തേയും സൂചിപ്പിക്കുന്നു
“π” ഗ്രീക്ക് അക്ഷരമാലയിലെ പതിനാറാമത്തെ അക്ഷരമാണ്. ഇത് ഗണിത ശാസ്ത്രത്തിലെ വളരെ പ്രസിദ്ധമായൊരു സ്ഥിരാങ്കത്തെ സൂചിപ്പിക്കുന്നു.
ഒരു വൃത്തത്തിന്റെ ചുറ്റളവിനെ അതിന്റെ വ്യാസം കൊണ്ടു ഹരിച്ചാല്( C/d ) കിട്ടുന്ന സ്ഥിരാങ്കമാണ് “π” . വൃത്തത്തിന്റെ വിസ്തീര്ണ്ണവും പരിധിയും കണ്ടുപിടിയ്ക്കാന് “π” കൂടിയേ കഴിയൂ. സാധാരണയായി നമ്മള് സ്വീകരിച്ചുവരുന്ന പൈയുടെ ഏകദേശമുല്യങ്ങള് 3.14 അല്ലെങ്കില് 22/7 എന്നീ ഭിന്നസംഖ്യകളാണ്. യഥാര്ത്ഥത്തില് “π” ഒരു അഭിന്നകമാണ് ( Irrational number). ഈ സ്ഥിരാങ്കത്തിന്റെ ദശാംശരൂപം അനന്തമായി നീണ്ടുപോകുന്നു.
വളരെക്കാലം മുന്പു തന്നെ ഈ സ്ഥിരാങ്കത്തിന്റെ യഥാര്ത്ഥ ദശാംശരൂപം കണ്ടെത്താന് ശ്രമങ്ങള് നടന്നിരുന്നതാണ്.ആര്ക്കിമിഡീസ് ആണ് ആദ്യമായി ഈ അനുപാതം ക്ണ്ടെത്തിയത്. ഈ ജിജ്ഞസയില് നമ്മുടെ രാജ്യവും ഒട്ടും പിന്നിലായിരുന്നില്ല. . ക്രിസ്തുവിനു മുന്പ് നാലാം നൂറ്റാണ്ടില് ആര്യഭടനും ക്രിസ്തുവിനുശേഷം പതിനാലാം നൂറ്റാണ്ടില് സംഗമഗ്രാമ മാധവന് എന്ന കേരളീയ ഗണിതശാസ്ത്രജ്ഞനും ഈ വഴിയില് സഞ്ചരിച്ചിരുന്നവരില് ചിലര് മാത്രം.ആദ്യമായി ആര്യഭടനാണ് വൃത്തപരിധിയെ വ്യാസംകൊണ്ടു ഹരിച്ചാല് കിട്ടുന്ന സ്ഥിരാങ്കം 3. 1416 ആണെന്നു കണ്ടെത്തിയത്. മാധവന് ആവിഷ്ക്കരിച്ച സൂത്രവാക്യം അനുസരിച്ച് 'പൈ'യുടെ ഏകദേശമൂല്യം 3.14159265359 ആണ്. പക്ഷേ മൂന്നു നൂറ്റാണ്ടുകള്ക്കു ശേഷം ജെയിംസ് ഗ്രിഗറി, ലെബനിറ്റ്സ്, ലാംബെര്ട്ട് തുടങ്ങിയ പാശ്ചാത്യ പണ്ഡിതര് ഇതേ ദിശയില് സഞ്ചരിച്ചു കണ്ടെത്തിയ പൈ മൂല്യമണ് ലോകം ഇന്നും അംഗീകരിച്ചിരിക്കുന്നത്. അതാകട്ടെ 3.1415926 എന്നതാണ്. (ഈ സംഖ്യ ഓര്ത്തിരിക്കാന് ഈ വാചകത്തിലെ വാക്കുകളുടെ അക്ഷരങ്ങളുടെ എണ്ണം നോക്കിയാല് മതി "Sir, I know a trick generates pi values" ). ഇന്നു കമ്പ്യൂടറിന്റെ സഹായത്തോടെ വളരെയധികം സ്ഥാനങ്ങള് ഉള്ള ദശാംശ പുലീകരണം പൈക്കു കണ്ടെത്തിയിട്ടുണ്ട്. ഈ പുലീകരണം ഒരിക്കലും അവസാനിക്കുന്നില്ല എന്നു മാത്രമല്ല ക്രമമായി ആവര്ത്തിക്കുന്നുമില്ല. അതിനാല് പൈ ഒരു അഭിന്നകമണെന്ന് (irrational number) ആണെന്ന് പറയാം.
എ.ഡി 800 നോടടുത്ത് ബാഗ്ദാദില് ജീവിച്ചിരുന്ന അല്-ഖവാരിസ്മി 3.1416 എന്ന വില കണ്ടെത്തിയിരുന്നു. അദ്ദേഹത്തിന്റെ "അല്-ജബര് വല് മുഖബ്ബല”എന്ന ഗണിശാസ്ത്ര ഗ്രന്ഥത്തില് നിന്നാണ് "അല്ജിബ്ര” എന്ന പേരു രൂപപ്പെട്ടത്. അതിനുശേഷം, ലെബനീസ്, ഡീമോര്ഗന്, ഓയ്ലര് തുടങ്ങി ധാരാളം മഹത്തുക്കള് π യുടെ കൂടുതല് കൃത്യമായ വിലകള്ക്കു വേണ്ടി ശ്രമിച്ചു. എ.ഡി. 1540 മുതല് 1610 വരെ ജീവിച്ചിരുന്ന ലുഡോള്ഫ് വാന് സ്യൂലെന് (Ludolph Van Ceulen)തന്റെ ജീവിതത്തിന്റെ സിംഹഭാഗവും ഇതിനായി മാറ്റിവെയ്ക്കുകയും 35 സ്ഥാനങ്ങള് വരെ (3.14159265358979323846264338327950288...) കണ്ടുപിടിക്കുകയും ചെയ്തു. അദ്ദേഹത്തിന്റെ ഈ അര്പ്പണബോധത്തെ മാനിച്ച്, ചിലപ്പോള് π യെ "ലുഡോള്ഫ് സ്ഥിരാങ്കം ”(Ludolph's Constant) എന്നും വിളിക്കാറുണ്ട്.
3.14 , 22/7 എന്നീ സംഖ്യകള്ക്ക് വര്ഷത്തിലെ രണ്ടു ദിവസങ്ങളോടുള്ല സാദൃശ്യം കൗതുകകരമാണ്. മാര്ച്ച് 14, ജൂലൈ 22 എന്നിവയാണ് ആ ദിനങ്ങള്. ഈദിവസങ്ങളെ പൈ ദിനങ്ങളായി ആഘോഷിക്കുന്നു. സാന്ഫ്രന്സിസ്കോയിലെ ഭൗതികശാസ്ത്രജ്ഞനായിരുന്നു ലാറി ഷാ 1988 ല് മാര്ച്ച് 14 ന് ആണ് ഈ ആഘോഷത്തിനു തുടക്കമിട്ടത്. അദ്ദേഹം ജോലി ചെയ്തിരുന്ന എക്സ്പ്ലോറടോറിയത്തില് സഹപ്രവര്ത്തകരോടൊപ്പം വൃത്താകാരത്തില് നടന്ന് പൈ എന്ന മധുരപലഹാരം ആസ്വദിച്ചുകൊണ്ടാണ് ആദ്യമായി പൈ ദിനം ആഘോഷിച്ചത്. അവര് പിന്നീട് ഇതു തുടര്ന്നു പോരുകയും ചെയ്തു. 2009 മാര്ച്ച് 12ന് ആണ് യു എസ് ഗവണ്മെന്റ് ഔദ്യോഗികമായി മാര്ച്ച് 14 ദേശീയ പൈ ദിനമായി പ്രഖ്യാപിച്ചത്. 2010 ല് ഗൂഗിള് ഈ ദിനത്തില് പ്രത്യേകമായൊരു ഡൂഡിള് തന്നെ അവതരിപ്പിക്കുകയുണ്ടായി. പൈ ഭക്ഷിച്ചുകൊണ്ടും ഗണിതശാസ്ത്രസംബന്ധിയായ മത്സരങ്ങളും പ്രബന്ധാവതരണവും ഒക്കെയായി വിവിധ രീതിയില് പൈ ദിനം ആഘോഷിക്കപ്പെടുന്നു. ക്രമേണ നമ്മുടെ നാട്ടിലും ഈ ആഘോഷങ്ങള് പച്ചപിടിച്ചു വരുന്നു.
2015 മാര്ച്ച് മാസം മുഴുവന് പൈ മാസമായി( 3.14) തന്നെ ആചരിക്കുകയുണ്ടായി. ഈ വര്ഷമാകട്ടെ പൈദിനം അതിവിശിഷ്ടമായ ദശാംശഘടനെയെ നല്കുന്നുമുണ്ട്. ഈ വര്ഷം, മാര്ച്ച് 14, 9 മണി 26 മിനുട്ട് 53 സെക്കണ്ട്. അതായത് 3.14 15 9 26 53. ആദ്യത്തെ പത്ത് അക്കങ്ങള് ആണ് പൈ വിപുലീകരണത്തില് ഇവിടെ ലഭ്യമായിരിക്കുന്നത്. ഇനി ഒരിക്കലും ഈ നൂറ്റാണ്ടില് ഇങ്ങനെ ഒരു സമയം ലഭ്യമല്ല തന്നെ.
വര്ഷത്തിലെ ആദ്യത്തെ പൈ ദിനമായ മാര്ച്ച് 14 നു വളരെ യാദൃശ്ചികമെങ്കിലും വേറൊരു പ്രത്യേകത കൂടിയുണ്ട്. അത് ഇരുപതാം നൂറ്റാണ്ടിലെ ഏറ്റവും പ്രതിഭാധനനായ ശാസ്ത്രഗവേഷകനായി പരക്കെ അംഗീകരിക്കപ്പെടുന്ന ശാസ്ത്രജ്ഞന് ആല്ബര്ട്ട് ഐന്സ്റ്റീന്റെ ജന്മദിനമാണന്ന്. 1879 മാര്ച്ച് 14 നാണ് അദ്ദേഹം ജര്മ്മനിയിലെ ഉല്മില് ഭൂജാതനായത്.
ഈ കൗതുകം നോക്കൂ, π യുടെ വില 400 സ്ഥാനങ്ങള്ക്ക് എഴുതിയാല്
3.14159265358979323846264338327950288419716939937510582097494459230781640628620899862803482534211706798214808651328230664709384460955058223172535940812848117450284102701938521105559644622948954930381964428810975665933446128475648233786783165271201909145648566923460348610454326648213393607260249141273724587006606315588174881520920962829254091715364367892590360011330530548820466521384146951941511609
{പൈദിനത്തോടു ബന്ധപ്പെട്ട മറ്റെരു ദിനമാണ് 'ടോ ദിനം'( Tau day- τ day.) (τ ഗ്രീക്ക് അക്ഷരമാലയിലെ 19 മത്തെ അക്ഷരമാണ്)
ടോ ദിനം ജൂണ് 28 ആണ് അതായത് 6. 28. ഇത് ( 3.14 X 2 ) . ഇതാകട്ടെ ഒരു വൃത്തത്തിന്റെ പരിധിയും ആരവും തമ്മിലുള്ല അനുപാതത്തിനു തുല്യമായിരിക്കും. അതായത് C/r.}
'
“π” ഗ്രീക്ക് അക്ഷരമാലയിലെ പതിനാറാമത്തെ അക്ഷരമാണ്. ഇത് ഗണിത ശാസ്ത്രത്തിലെ വളരെ പ്രസിദ്ധമായൊരു സ്ഥിരാങ്കത്തെ സൂചിപ്പിക്കുന്നു.
ഒരു വൃത്തത്തിന്റെ ചുറ്റളവിനെ അതിന്റെ വ്യാസം കൊണ്ടു ഹരിച്ചാല്( C/d ) കിട്ടുന്ന സ്ഥിരാങ്കമാണ് “π” . വൃത്തത്തിന്റെ വിസ്തീര്ണ്ണവും പരിധിയും കണ്ടുപിടിയ്ക്കാന് “π” കൂടിയേ കഴിയൂ. സാധാരണയായി നമ്മള് സ്വീകരിച്ചുവരുന്ന പൈയുടെ ഏകദേശമുല്യങ്ങള് 3.14 അല്ലെങ്കില് 22/7 എന്നീ ഭിന്നസംഖ്യകളാണ്. യഥാര്ത്ഥത്തില് “π” ഒരു അഭിന്നകമാണ് ( Irrational number). ഈ സ്ഥിരാങ്കത്തിന്റെ ദശാംശരൂപം അനന്തമായി നീണ്ടുപോകുന്നു.
വളരെക്കാലം മുന്പു തന്നെ ഈ സ്ഥിരാങ്കത്തിന്റെ യഥാര്ത്ഥ ദശാംശരൂപം കണ്ടെത്താന് ശ്രമങ്ങള് നടന്നിരുന്നതാണ്.ആര്ക്കിമിഡീസ് ആണ് ആദ്യമായി ഈ അനുപാതം ക്ണ്ടെത്തിയത്. ഈ ജിജ്ഞസയില് നമ്മുടെ രാജ്യവും ഒട്ടും പിന്നിലായിരുന്നില്ല. . ക്രിസ്തുവിനു മുന്പ് നാലാം നൂറ്റാണ്ടില് ആര്യഭടനും ക്രിസ്തുവിനുശേഷം പതിനാലാം നൂറ്റാണ്ടില് സംഗമഗ്രാമ മാധവന് എന്ന കേരളീയ ഗണിതശാസ്ത്രജ്ഞനും ഈ വഴിയില് സഞ്ചരിച്ചിരുന്നവരില് ചിലര് മാത്രം.ആദ്യമായി ആര്യഭടനാണ് വൃത്തപരിധിയെ വ്യാസംകൊണ്ടു ഹരിച്ചാല് കിട്ടുന്ന സ്ഥിരാങ്കം 3. 1416 ആണെന്നു കണ്ടെത്തിയത്. മാധവന് ആവിഷ്ക്കരിച്ച സൂത്രവാക്യം അനുസരിച്ച് 'പൈ'യുടെ ഏകദേശമൂല്യം 3.14159265359 ആണ്. പക്ഷേ മൂന്നു നൂറ്റാണ്ടുകള്ക്കു ശേഷം ജെയിംസ് ഗ്രിഗറി, ലെബനിറ്റ്സ്, ലാംബെര്ട്ട് തുടങ്ങിയ പാശ്ചാത്യ പണ്ഡിതര് ഇതേ ദിശയില് സഞ്ചരിച്ചു കണ്ടെത്തിയ പൈ മൂല്യമണ് ലോകം ഇന്നും അംഗീകരിച്ചിരിക്കുന്നത്. അതാകട്ടെ 3.1415926 എന്നതാണ്. (ഈ സംഖ്യ ഓര്ത്തിരിക്കാന് ഈ വാചകത്തിലെ വാക്കുകളുടെ അക്ഷരങ്ങളുടെ എണ്ണം നോക്കിയാല് മതി "Sir, I know a trick generates pi values" ). ഇന്നു കമ്പ്യൂടറിന്റെ സഹായത്തോടെ വളരെയധികം സ്ഥാനങ്ങള് ഉള്ള ദശാംശ പുലീകരണം പൈക്കു കണ്ടെത്തിയിട്ടുണ്ട്. ഈ പുലീകരണം ഒരിക്കലും അവസാനിക്കുന്നില്ല എന്നു മാത്രമല്ല ക്രമമായി ആവര്ത്തിക്കുന്നുമില്ല. അതിനാല് പൈ ഒരു അഭിന്നകമണെന്ന് (irrational number) ആണെന്ന് പറയാം.
എ.ഡി 800 നോടടുത്ത് ബാഗ്ദാദില് ജീവിച്ചിരുന്ന അല്-ഖവാരിസ്മി 3.1416 എന്ന വില കണ്ടെത്തിയിരുന്നു. അദ്ദേഹത്തിന്റെ "അല്-ജബര് വല് മുഖബ്ബല”എന്ന ഗണിശാസ്ത്ര ഗ്രന്ഥത്തില് നിന്നാണ് "അല്ജിബ്ര” എന്ന പേരു രൂപപ്പെട്ടത്. അതിനുശേഷം, ലെബനീസ്, ഡീമോര്ഗന്, ഓയ്ലര് തുടങ്ങി ധാരാളം മഹത്തുക്കള് π യുടെ കൂടുതല് കൃത്യമായ വിലകള്ക്കു വേണ്ടി ശ്രമിച്ചു. എ.ഡി. 1540 മുതല് 1610 വരെ ജീവിച്ചിരുന്ന ലുഡോള്ഫ് വാന് സ്യൂലെന് (Ludolph Van Ceulen)തന്റെ ജീവിതത്തിന്റെ സിംഹഭാഗവും ഇതിനായി മാറ്റിവെയ്ക്കുകയും 35 സ്ഥാനങ്ങള് വരെ (3.14159265358979323846264338327950288...) കണ്ടുപിടിക്കുകയും ചെയ്തു. അദ്ദേഹത്തിന്റെ ഈ അര്പ്പണബോധത്തെ മാനിച്ച്, ചിലപ്പോള് π യെ "ലുഡോള്ഫ് സ്ഥിരാങ്കം ”(Ludolph's Constant) എന്നും വിളിക്കാറുണ്ട്.
3.14 , 22/7 എന്നീ സംഖ്യകള്ക്ക് വര്ഷത്തിലെ രണ്ടു ദിവസങ്ങളോടുള്ല സാദൃശ്യം കൗതുകകരമാണ്. മാര്ച്ച് 14, ജൂലൈ 22 എന്നിവയാണ് ആ ദിനങ്ങള്. ഈദിവസങ്ങളെ പൈ ദിനങ്ങളായി ആഘോഷിക്കുന്നു. സാന്ഫ്രന്സിസ്കോയിലെ ഭൗതികശാസ്ത്രജ്ഞനായിരുന്നു ലാറി ഷാ 1988 ല് മാര്ച്ച് 14 ന് ആണ് ഈ ആഘോഷത്തിനു തുടക്കമിട്ടത്. അദ്ദേഹം ജോലി ചെയ്തിരുന്ന എക്സ്പ്ലോറടോറിയത്തില് സഹപ്രവര്ത്തകരോടൊപ്പം വൃത്താകാരത്തില് നടന്ന് പൈ എന്ന മധുരപലഹാരം ആസ്വദിച്ചുകൊണ്ടാണ് ആദ്യമായി പൈ ദിനം ആഘോഷിച്ചത്. അവര് പിന്നീട് ഇതു തുടര്ന്നു പോരുകയും ചെയ്തു. 2009 മാര്ച്ച് 12ന് ആണ് യു എസ് ഗവണ്മെന്റ് ഔദ്യോഗികമായി മാര്ച്ച് 14 ദേശീയ പൈ ദിനമായി പ്രഖ്യാപിച്ചത്. 2010 ല് ഗൂഗിള് ഈ ദിനത്തില് പ്രത്യേകമായൊരു ഡൂഡിള് തന്നെ അവതരിപ്പിക്കുകയുണ്ടായി. പൈ ഭക്ഷിച്ചുകൊണ്ടും ഗണിതശാസ്ത്രസംബന്ധിയായ മത്സരങ്ങളും പ്രബന്ധാവതരണവും ഒക്കെയായി വിവിധ രീതിയില് പൈ ദിനം ആഘോഷിക്കപ്പെടുന്നു. ക്രമേണ നമ്മുടെ നാട്ടിലും ഈ ആഘോഷങ്ങള് പച്ചപിടിച്ചു വരുന്നു.
2015 മാര്ച്ച് മാസം മുഴുവന് പൈ മാസമായി( 3.14) തന്നെ ആചരിക്കുകയുണ്ടായി. ഈ വര്ഷമാകട്ടെ പൈദിനം അതിവിശിഷ്ടമായ ദശാംശഘടനെയെ നല്കുന്നുമുണ്ട്. ഈ വര്ഷം, മാര്ച്ച് 14, 9 മണി 26 മിനുട്ട് 53 സെക്കണ്ട്. അതായത് 3.14 15 9 26 53. ആദ്യത്തെ പത്ത് അക്കങ്ങള് ആണ് പൈ വിപുലീകരണത്തില് ഇവിടെ ലഭ്യമായിരിക്കുന്നത്. ഇനി ഒരിക്കലും ഈ നൂറ്റാണ്ടില് ഇങ്ങനെ ഒരു സമയം ലഭ്യമല്ല തന്നെ.
വര്ഷത്തിലെ ആദ്യത്തെ പൈ ദിനമായ മാര്ച്ച് 14 നു വളരെ യാദൃശ്ചികമെങ്കിലും വേറൊരു പ്രത്യേകത കൂടിയുണ്ട്. അത് ഇരുപതാം നൂറ്റാണ്ടിലെ ഏറ്റവും പ്രതിഭാധനനായ ശാസ്ത്രഗവേഷകനായി പരക്കെ അംഗീകരിക്കപ്പെടുന്ന ശാസ്ത്രജ്ഞന് ആല്ബര്ട്ട് ഐന്സ്റ്റീന്റെ ജന്മദിനമാണന്ന്. 1879 മാര്ച്ച് 14 നാണ് അദ്ദേഹം ജര്മ്മനിയിലെ ഉല്മില് ഭൂജാതനായത്.
ഈ കൗതുകം നോക്കൂ, π യുടെ വില 400 സ്ഥാനങ്ങള്ക്ക് എഴുതിയാല്
3.14159265358979323846264338327950288419716939937510582097494459230781640628620899862803482534211706798214808651328230664709384460955058223172535940812848117450284102701938521105559644622948954930381964428810975665933446128475648233786783165271201909145648566923460348610454326648213393607260249141273724587006606315588174881520920962829254091715364367892590360011330530548820466521384146951941511609
{പൈദിനത്തോടു ബന്ധപ്പെട്ട മറ്റെരു ദിനമാണ് 'ടോ ദിനം'( Tau day- τ day.) (τ ഗ്രീക്ക് അക്ഷരമാലയിലെ 19 മത്തെ അക്ഷരമാണ്)
ടോ ദിനം ജൂണ് 28 ആണ് അതായത് 6. 28. ഇത് ( 3.14 X 2 ) . ഇതാകട്ടെ ഒരു വൃത്തത്തിന്റെ പരിധിയും ആരവും തമ്മിലുള്ല അനുപാതത്തിനു തുല്യമായിരിക്കും. അതായത് C/r.}
'

ഒരു പൈയുടെ പിന്നില് ഇത്രയും രഹസ്യങ്ങളുണ്ടായിരുന്നോ!
ReplyDeleteവളരെ നന്ദി സര്. സന്തോഷം, സ്നേഹം..
Deleteവിജ്ഞാനപ്രദം!
ReplyDeleteആശംസകള്
വളരെ നന്ദി സര്. സന്തോഷം, സ്നേഹം..
Delete